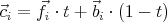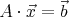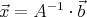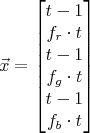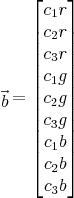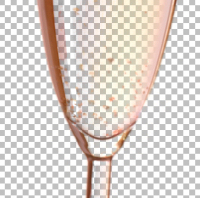Seit einiger Zeit arbeite ich nebenher an einem einfachen Verfahren zur Fotografie transparenter Gegenstände. Da die Ergebnisse inzwischen recht gut sind, möchte ich das Verfahren hier in einer Art Blog vorstellen. Da eine ordentliche Dokumentation viel Zeit benötigt, geschieht die Veröffentlichung der einzelnen Abschnitte Stück für Stück. Der aktuelle Stand ist vom 19. Jan. 2011

Einleitung

Motive wie Gläser, Vasen oder Flaschen zu fotografieren, stellt den Fotograf vor ein Problem: Die Tranzparenzeigenschaft des aufgenommenen Objektes geht durch die Fotografie verloren, das Motiv "verschmilzt" mit dem Hintergrund. Soll das Motiv - beispielsweise für Produkt-Präsentation - mit Hilfe von digitaler Bildbearbeitung in eine andere Szene hinein montiert werden, muss es aufwendig freigestellt werden.

Abb. 1

Abb. 2

Abbildung 1 verdeutlicht die Probleme, die beim manuellen Freistellen eines transparenten Objektes auftreten: Der - in diesem Beispiel blaue - Hintergrund ist durch das Objekt hindurch sichtbar und verfälscht so dessen eigentliche Farbe. Der Bildbearbeiter muss diese Verfärbung im Zuge der Freistellung mit geeigneten Werkzeugen korrigieren und in einem weiteren Bearbeitungsschritt händisch Transparenzinformationen in das Bild einfügen, z.B. durch nachträgliche Erstellung einer Alpha-Maske oder durch Anwendung von Löschpinseln. Besonders filigranen Bildstrukturen wie der Glasrand und komplexe Transparenzeffekte wie sie im Glasboden des Motives zu sehen sind, stellen bei diesen Verfahren jedoch auch erfahrene Bildbearbeiter vor eine Herausforderung.

Das Motiv in Abbildung 2 wurde hingegen mit dem Verfahren freigestellt, das ich hier vorstellen möchte. Die Objekte verfügen ohne aufwendige manuelle Nachbearbeitung über realistische Farb- und Transparenzinformationen und auch komplexe Effekte, wie das durchscheinende Etikett auf der dem Fotograf abgewandten Seite der Flasche oder die feinen Strukturen des Sektglases, kommen sehr gut zur Geltung. Weitere Ergebnisse sind am Ende der Seite zu finden.

Grundlagen

Bevor ich auf das eigentliche Verfahren eingehe, möchte ich zunächst ein paar Begriffe und Grundlagen erklären.

Digitale Fotos setzen sich kleinen, farbigen Bildpunkten zusammen, den so genannten Pixeln. Mit genügend Abstand zum Display betrachtet, verschmelzen diese Bildpunkte zu einem kontinuierlichen Bild. Bei Betrachtung des digitalen Bildes mit Hilfe einer Lupe werden die einzelnen Pixel jedoch sichtbar. Handelt es sich bei dem Display um einen alten Röhren-Monitor, so offenbart sich zudem eine weitere Eigenschaft von Pixeln: Sie setzen sich aus den drei Grundfarben der additiven Farbmischung zusammen: Rot, Grün und Blau. Alle Farben, die das Display darstellt, werden aus diesen drei Grundfarben gemischt: Gelb ist beispielsweise eine Mischung aus Rot und Grün (r=1, g=1, b=0), Türkies eine Mischfarbe aus Grün und Blau (r=0, g=1, b=1). Werden alle drei Farben mit voller Intensität zusammen gemischt, so ist das Ergebnis Weiß (1, 1, 1). Zur Notation: Farben werden hier als 3-Tupel angegeben, wobei die einzelnen Farbkomponenten - also Rot oder Grün oder Blau - aus dem Wertebereich [0, 1] stammen. Ein mittleres Grau hätte dementsprechend die Farbwerte (0.5, 0.5, 0.5) und ein Grau, dass leicht ins Bläuchliche geht die Farbwerte (0.5, 0.5, 0.7).

Für das vorgestellte Verfahren wird angenommen, dass jedes Foto aus einem Objekt im Vordergrund - dem Motiv - und einem Hintergrund besteht. Falls das Motiv vollständig nicht-transparent ist, wie beispielsweise ein Apfel, so ist jeder Pixel des Bildes entweder Teil des Bildhintergrundes oder Teil des Motives. Anders verhält es sich, wenn ein transparentes Objekt fotografiert wird: Pixel an transparenten Stellen des Motives können nun Anteile der Hintergrundfarbe enthalten. Je stärker die Transparenz des Objektes, desto mehr setzt sich die Farbe des Hintergrundes durch, je weniger das Objekt transparent ist, desto mehr kommt die eigentliche Farbe des Objektes zur Geltung. Ziel des Verfahrens ist es nun, für jeden Pixel im Bild abzuschätzen, wie groß der Anteil der Hintergrundfarbe an der Pixelfarbe ist, was uns wiederum Rückschlüsse auf die Stärke der Transparenz und die Farbe des Motives erlaubt.

Abb. 3

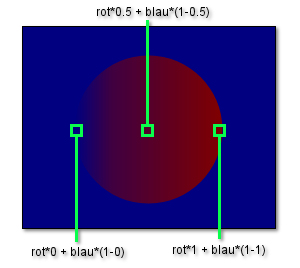
Abbildung 3 zeigt zur Verdeutlichung ein Bild mit einem blauen Hintergrund und einem roten Kreis als Motiv, wobei das Motiv von rechts nach links gleichmäßig an Transparenz zunimmt. In diesem Bild sind drei "Messpunke" markiert, der erste am linken Rand des Kreises, der zweite in der Mitte des Kreises und der dritte am rechten Rand. Der RGB-Wert der Farbe am ersten Messpunkt ist (0, 0, 1), da das Motiv an dieser Stelle zu 100% transparent ist und keinen Einfluss auf die gemessene Farbe hat. Anders beim zweiten Messpunkt, dort beträgt die Transparenz des Motives 50%, womit sich der Breitrag der Motivfarbe zum gemessenen Ergebnis eben auf diese 50% beläuft. Der RGB-Wert an dieser Stelle ist somit (0.5, 0, 0.5). Der dritte und letzte Messpunkt liefert den RGB-Wert (1, 0, 0), da die Transparenz des Motives bei dieser Messung nun 0% beträgt und der Hintergrund somit keinen Einfluss mehr auf die gemessene Farbe hat.

Mathematisch bedeutet diese Beobachtung, dass sich die Farbe eines Pixels (im Folgenden mit dem Buchstaben c für color bezeichnet) mit folgender Formel berechnen lässt:

(1)

Der Buchstabe f steht in dieser Gleichung für die Vordergrundfarbe (foreground) bzw. die Farbe des Motives an diesem Pixel. Der Buchstabe b steht für die Farbe des Hintergrundes (background). Sowohl c als auch f und b stellen also RGB-Farbwerte dar, und werden deswegen als Vektoren notiert, deren Komponenten die drei Farbkomponenten Rot, Grün und Blau repräsentieren. Der Buchstabe t stellt dar, wie stark die Transparenz des Objektes an der gemessenen Stelle ist: Je weiter sich der Wert von t der 1 nähert, desto mehr fällt die Farbe des Motives ins Gewicht - und um so weniger ist das Objekt folglich transparent. Je mehr sich t der 0 annähert, desto stärker wird analog dazu der Einfluss der Hintergrundes und somit der Grad der Transparenz. t ist folglich eine Art Mischverhältnis zwischen dem Vordergrund und dem Hintergrund.

Ziel des Verfahrens ist somit die Berechnung oder Schätzung der Werte für f und t. Sind diese beiden Informationen an jedem Pixel eines Bildes bestimmbar, so kann daraus ein neues Bild generiert werden, das ausschließlich das Motiv enthält und zudem über Transparenzinformationen in Form eines Alphakanals verfügt.

Wären die konkreten Werte für f, c und b an einem Pixel bekannt, könnte dieses Mischverhältnis t durch einfaches Umformen der Gleichung direkt berechnet werden. Genau an dieser Stelle wird der Kern des Problemes sichtbar: Weder die Farbe des Motives (also f) noch die Farbe des Hintergrundes (also b) sind bekannt, sondern lediglich eine Mischung aus beiden Farben mit unbekanntem Verhältnis. Die Gleichung ist nach keinem der Bestandteile eindeutig auflösbar, man spricht in diesem Fall von einem unterbestimmten mathematischen Problem.

Freistellungsverfahren

Nehmen wir nun an, der Fotograf hätte während der Aufnahme des Fotos einen matten, einfarbigen Karton hinter das Motiv gehalten. Wäre uns nun die Farbe des Kartons bekannt, könnten wir somit in etwa abschätzen, welche Farbe der Hintergrund b an einer beliebigen Stelle des Bildes hat -- nämlich ungefähr die Farbe des Kartons. Durch diesen Trick wäre es somit möglich, die Anzahl der unbekannten Variablen in der Gleichung auf zwei zu reduzieren: f und t. Damit ist die Gleichung allerdings weiterhin unterbestimmt und nicht eindeutig lösbar.

Der gängige Weg zur Lösung dieser Art von Problemen ist die Aufstellung eines Gleichungssystems: Statt eine einzelne Gleichung zu betrachten, wird versucht, mehrere, von einander verschiedene Gleichungen zu betrachten, die zusammen den gesuchten mathematischen Sachverhalt beschreiben. In unserem Fall erhalten wir die zusätzlichen Gleichungen einfach durch die Aufnahme weiterer Fotos. Dabei ist darauf zu achten, dass weder Kamera noch Motiv zwischen den einzelnen Aufnahmen bewegt werden und Belichtungszeit, Blende und Brennweite bei allen Aufnahmen gleich sind. Dies ist notwendig, damit die jeweils entstehenden Fotos (oder "Messungen") abgesehen von technisch bedingtem Rauschen unter absolut identischen Bedingungen aufgenommen werden. Jedes dieser Fotos erweitert das gesuchte Gleichungssystem also um eine weitere Gleichung und somit um zusätzliche Information, die zu einer eindeutigen Lösbarkeit des Gleichungssystems beiträgt. Um wirklich zusätzliche Information beisteuern zu können, müssen sich die einzelnen Gleichungen jeweils in ihren Parametern unterscheiden. Um dies sicher zu stellen muss pro Messung - also pro Foto - einer der Parameter f, t oder b variiert werden. Der einzige Parameter, der während der Aufnahme der Fotos tatsächlich beeinflusst werden kann, ist der Hintergrund des Bildes, b. Dies kann einfach durch mehrere farbige Kartons als Hintergrund erreicht werden. Die Parameter f und t sind für jede Aufnahme der Szene konstant und beschreiben damit für jeden Punkt im Bild genau den mathematischen Zusammenhang, den wir ermitteln wollen. Im Folgenden wird davon ausgegangen, dass drei Fotos - also drei Gleichungen - ausreichen, um das gesamte Gleichungssystem eindeutig zu bestimmen.

(2)

(3)

Achtung: Der Artikel nutzt ab hier mehrdeutige Bezeichner. Zum einen ist vom Ergebnisvektor b und von der Bildhintergrundfarbe b die Rede. Von welchem b an gegebener Stelle die Rede ist sollte aus dem Kontext heraus klar sein, ich werde die Grafiken und den Text bei gegebener Zeit dennoch überarbeiten um die Leserlichkeit zu verbessern.

Um das Gleichungssystem lösen zu können, muss es in eine Matrixform wie in Gleichung (2) überführt werden. Für jeden einzelnen Pixel im Ergebnisbild muss dieses Gleichungssystem nach x aufgelöst werden, wie es in Gleichung (3) zu sehen ist. Die einzelnen Matrizen dieses Gleichungssystems werden an dieser Stelle kurz beschrieben.



Das dargestellte Gleichungssystem besteht aus drei Fotos. Da die drei Farbkomponenten separat behandelt werden, ergeben sich aus den drei Fotos insgesamt 3x3=9 Gleichungen. Seien c1, c2 und c3 nun die Pixelfarben für alle drei Bilder an einer gegebenen, für allen drei Bildern identischen, (x,y)-Koordinate. Alle drei dieser Variablen bestehen aus den drei Farbkomponenten Rot, Grün und Blau, so dass gilt:



Der Ergebnisvektor b setzt sich aus diesen Farbkomponenten zusammen: Die ersten drei Elemente entsprechen den Rot-Komponenten der Bilder 1, 2 und 3, die Elemente 4 bis 6 der Grün-Komponente und die restlichen drei Elemente der Blau-Komponente der drei Farbwerte.

Die Matrix A und der Vektor x sind nun gerade so gewählt, dass zum einen die Multiplikation von A und x den Ergebnisvektor b erzeugt und zum anderen der Vektor x als einziges Element der Gleichung Vorkommen der Variablen t und f beinhaltet.

(4)

Die vollständige Gleichung ist in (4) zu sehen. Wie weiter oben bereits beschrieben, können wir vereinfachend davon ausgehen, dass die Farbe des Bildhintergrundes für alle drei Fotos bekannt ist. Somit sind wir in der Lage, die Matrix A konkret anzugeben. Der Ergebnisvektor b setzt sich aus den Farbwerten c1, c2 und c3 zusammen - auch diese Werte können wir konkret angeben und somit den gesamten Vektor b.

Sind A und b bestimmt, kann die Gleichung (2) mit Hilfe numerischer Verfahren nach x aufgelöst werden. Der gesuchte Wert für die Transparenzinformation t kann nun einfach durch



berechnet werden, wobei x[0] dem ersten Element des Vektors x entspricht. Der Wert für die Farbe des Motives f ergibt sich nun durch Einsetzen der Werte t, c und b in die Gleichung (1) und Umstellung der Gleichung nach f.

Implementierung

Eine detaillierte Dokumentation der Implementierung folgt.

Zum Schluss möchte ich hier noch einige Ergebnisbilder zeigen. Alle Objekte wurden mit dem vorgestellten Verfahren freigestellt und in ein anderes Bild hinein montiert. Mehr Informationen zu den einzelnen Bildern folgen in Kürze.